There are no changing magnetic fields in the problem, so we can apply Kirchhoff's Law around the loop.
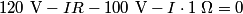 where we have modeled the battery as an ideal voltage source of 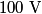 in series with a resistor of in series with a resistor of 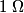 . We are given that . We are given that 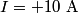 (the problem statement does not explicitly tell us in which direction the (the problem statement does not explicitly tell us in which direction the 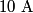 current is flowing, but if the current is assumed to flow in counterclockwise direction, then the resistance current is flowing, but if the current is assumed to flow in counterclockwise direction, then the resistance 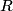 turns out to be negative, which is absurd) and from this we can find the value of turns out to be negative, which is absurd) and from this we can find the value of 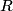 : :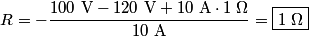 Therefore, answer (C) is correct. |